Sistemul de inegalități este o soluție. Sistem de inegalități liniare

Inegalitățile și inegalitățile sunt unul dintrecel care are loc în liceu în algebră. La nivel de complexitate, nu este cel mai dificil, deoarece are reguli simple (despre ei puțin mai târziu). De regulă, elevii pot rezolva cu ușurință sistemul de inegalități. Acest lucru se datorează și faptului că profesorii pur și simplu "instruiesc" studenții lor pe această temă. Și nu pot face acest lucru, deoarece este studiat în viitor cu alte cantități matematice și este verificat și pentru OGE și USE. În manualele școlare, subiectul inegalităților și inegalităților este descris în detaliu, deci dacă o veți studia, este mai bine să le recurgeți. Acest articol redă numai materialele mari, iar în ea pot exista omisiuni.

Conceptul unui sistem de inegalități

Dacă te întorci la limba științifică, poți dadefinirea conceptului de "sistem de inegalități". Acesta este un model matematic care reprezintă mai multe inegalități. Din acest model, desigur, ea are nevoie de o soluție, și în capacitatea sa de a acționa ca un răspuns comun pentru toate inegalitățile sistemului propus în loc de muncă (de obicei în ea și să scrie, de exemplu: „Rezolvați sistemul de inegalități 4 x + 1> 2 și 30 - x > 6 ... "). Cu toate acestea, înainte de a trece la tipurile și metodele de soluționare, trebuie să găsim ceva.

Sistemele de inegalități și sistemul de ecuații

În procesul de a studia un subiect nou foarte desexistă neînțelegeri. Pe de o parte, totul este clar și mai degrabă vrea să înceapă rezolvarea sarcinilor, iar pe de altă parte - câteva momente rămân în "umbra", nu prea bine înțelese. De asemenea, unele elemente ale cunoștințelor deja dobândite pot fi interconectate cu altele noi. Ca rezultat al acestei "suprapuneri", apar adesea greșeli.

Prin urmare, înainte de a începe analiza noastrăsubiect, ar trebui să vă amintiți despre diferențele dintre ecuații și inegalități, sistemele lor. Pentru a face acest lucru, trebuie să explicăm încă o dată ce sunt conceptele matematice. Ecuația este întotdeauna egalitatea și este întotdeauna ceva egal (în matematică acest cuvânt este notat cu semnul "="). Inegalitatea este un model în care o cantitate sau mai mult sau mai puțin decât alta sau conține afirmația că nu sunt aceleași. Astfel, în primul caz, este necesar să se vorbească despre egalitate, iar în cel de-al doilea caz, oricât de evident ar putea fi din titlu, inegalitatea datelor originale. Sistemele de ecuații și inegalități practic nu diferă una de alta și metodele de rezolvare a acestora sunt aceleași. Singura diferență este că în primul caz folosim egalități, în timp ce în cea de-a doua inegalitate se utilizează.

Tipuri de inegalități

Există două tipuri de inegalități: numeric și cu variabilă necunoscută. Primul tip reprezintă valorile furnizate (cifre) inegale unele de altele, de exemplu 8> 10. Al doilea este inegalitățile care conțin o variabilă necunoscută (notată cu o literă a alfabetului latin, cel mai adesea X). Această variabilă necesită locația sa. În funcție de cât de multe există, în modelul matematic există inegalități cu unul (constituie un sistem de inegalități cu o variabilă) sau mai multe variabile (constituie un sistem de inegalități cu mai multe variabile).

Ultimele două specii în funcție de gradul de construcție și denivelul de complexitate al deciziei este împărțit în simplu și complex. Simple sunt de asemenea numite inegalități liniare. Ele, la rândul lor, sunt împărțite în stricte și nestricătoare. Strict specific "spune" că o valoare trebuie să fie mai mică sau mai mare, deci aceasta este o inegalitate pură. Există câteva exemple: 8 x + 9> 2, 100 - 3 x> 5 și așa mai departe. Aceasta înseamnă că o valoare poate fi mai mare sau egală cu o altă valoare (semnul "≥") sau mai mică sau egală cu o altă valoare (semnul "≤"). Chiar și în inegalitățile liniare, variabila nu este în rădăcină, în pătrat, nu este împărțită în nimic, din cauza a ceea ce se numește "simplu". Variabilele complexe includ variabile necunoscute, a căror constatare necesită efectuarea mai multor operații matematice. Acestea sunt adesea situate într-un pătrat, un cub sau sub rădăcină, pot fi modulare, logaritmice, fracționare etc. Dar, deoarece sarcina noastră este să înțelegem soluția sistemelor de inegalități, vom vorbi despre sistemul inegalităților liniare. Cu toate acestea, înainte de aceasta, ar trebui spus câteva cuvinte despre proprietățile lor.

Proprietăți de inegalitate

Proprietățile inegalităților includ următoarele:

1. Semnul de inegalitate este inversat dacă se utilizează o operațiune pentru a schimba secvența părților (de exemplu, dacă t₁ ≤ t₂apoi t₂ ≥ t₁).
2. Ambele părți ale inegalității permit să se adauge același număr (de exemplu, dacă t₁ ≤ t₂apoi t₁ + număr ≤ t₂ + număr).
3. Două sau mai multe inegalități cu semnul aceleiași direcții vă permit să adăugați părțile stângi și drepte (de exemplu, dacă t₁ ≥ T₂, t₃ ≥ T₄apoi t₁ + t₃ ≥ T₂ + t₄).
4. Ambele părți ale inegalității vă permit să vă multiplicați sau să împărțiți cu același număr pozitiv (de exemplu, dacă t₁ ≤ t₂ și numărul ≤ 0, atunci numărul · t₁ ≥ numărul · t₂).
5. Două sau mai multe inegalități cu termeni pozitivi și un semn al unei direcții permit să se înmulțească unul pe altul (de exemplu, dacă t₁ ≤ t₂, t₃ ≤ t₄, t₁, t₂, t₃, t₄ ≥ 0 atunci t₁ · T₃ ≤ t₂ · T₄).
6. Ambele părți ale inegalității se înmulțesc sau se împart în același număr negativ, dar inegalitatea se schimbă (de exemplu, dacă t₁ ≤ t₂ și numărul ≤ 0, atunci numărul · t₁ ≥ numărul · t₂).
7. Toate inegalitățile au proprietatea tranzitivității (de exemplu, dacă t₁ ≤ t₂ și t₂ ≤ t₃apoi t₁ ≤ t₃).

Acum, după studierea principiilor de bază ale teoriei referitoare la inegalități, putem trece direct la luarea în considerare a regulilor de rezolvare a sistemelor lor.

Rezolvarea sistemelor de inegalitate. Informații generale. moduri de a rezolva

După cum sa menționat mai sus, decizia estevalori variabile care se potrivesc tuturor inegalităților unui sistem dat. Soluția sistemelor de inegalitate este implementarea operațiunilor matematice care, în cele din urmă, conduc la soluția întregului sistem sau dovedește că nu are soluții. În acest caz, se spune că variabila se referă la un set numeric gol (scris ca: scrisoare variabilă ∈ (semnul "aparține") ø (semnul "gol"set "), de exemplu, x ∈ ø (citește astfel:" Variabila "X aparține setului gol") Există mai multe modalități de a rezolva sisteme de inegalitate: grafică, algebrică, substituție. au mai multe variabile necunoscute. În cazul în care există doar una, se va face metoda intervalului.

Mod grafic

Permite rezolvarea unui sistem de inegalități cu mai multevalori necunoscute (de la doi la mai sus). Datorită acestei metode, sistemul de inegalități liniare este rezolvat destul de ușor și rapid, deci este metoda cea mai comună. Acest lucru se datorează faptului că plotarea reduce cantitatea de scriere a operațiilor matematice. În special devine plăcut să scăpați puțin de stilou, să ridicați un creion cu un conducător și să începeți alte acțiuni cu ajutorul lor, când ați făcut multe lucruri și doriți o mică varietate. Cu toate acestea, unii oameni nu le place această metodă datorită faptului că trebuie să se desprindă de sarcină și să schimbe activitatea mentală în desen. Cu toate acestea, acesta este un mod foarte eficient.

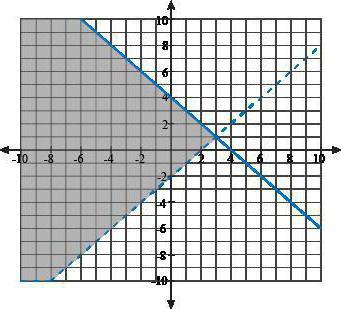
Pentru a realiza soluția sistemului de inegalități cufolosind metoda grafică, este necesar să transferăm toți membrii fiecărei inegalități spre partea stângă. Semnele vor fi inversate, dreptul va fi scos la zero, atunci trebuie să scrieți fiecare inegalitate separat. Ca urmare, inegalitățile au ca rezultat funcții. După aceea, puteți obține un creion și un riglă: acum trebuie să desenați un grafic al fiecărei funcții obținute. Întregul set de numere, care va fi în intervalul de intersecție, va fi o soluție la sistemul de inegalități.

Metoda algebrică

Vă permite să rezolvați un sistem de inegalități cu douăvariabile necunoscute. De asemenea, inegalitățile trebuie să aibă același semn de inegalitate (adică ele trebuie să conțină doar semnul "mai mult" sau doar semnul "mai puțin") etc. În ciuda limitărilor sale, această metodă este și mai complexă. Se aplică în două etape.

Primul include acțiunea de a scăpauna dintre variabilele necunoscute. Mai întâi trebuie să o selectați, apoi să verificați prezența numerelor în fața acestei variabile. Dacă acestea nu sunt (atunci variabila va arăta ca o singură literă), atunci nu schimbăm nimic, dacă există (tipul variabilei va fi, de exemplu, 5y sau 12y), atunci este necesar să vă asigurați că în fiecare inegalitate numărul înainte de variabila selectată este la fel. Pentru a face acest lucru, multiplicați fiecare membru al inegalităților printr-un factor comun, de exemplu, dacă 3y este scris în prima inegalitate și 5y în al doilea, atunci toți membrii primei inegalități se înmulțesc cu 5, iar al doilea cu 3. Se vor împlini 15y și 15y, respectiv.

A doua etapă a deciziei. Este necesar să transferați partea stângă a fiecărei inegalități în părțile drepte, cu o schimbare a semnului fiecărui membru în celălalt, pentru a scrie în dreapta. Apoi vine cel mai interesant lucru: scăderea variabilei selectate (cu alte cuvinte, aceasta se numește "reducere") în timpul plierea inegalităților. Rezultatul este o inegalitate cu o variabilă care trebuie rezolvată. După aceasta, ar trebui să faceți același lucru, numai cu altă variabilă necunoscută. Rezultatele vor fi soluția sistemului.

Metoda de substituție

Vă permite să rezolvați un sistem de inegalități în prezența luicapacitatea de a introduce o nouă variabilă. De obicei, această metodă este folosită atunci când o variabilă necunoscută într-un membru al inegalității este ridicată la puterea a patra, iar în celălalt membru are un pătrat. Astfel, această metodă vizează reducerea gradului de inegalitate în sistem. Exemplu x Inegalitate⁴ - x² - 1 ≤ 0 în acest fel este rezolvată după cum urmează. Se introduce o nouă variabilă, de exemplu, t. Ei scriu: "Fie t = x²", atunci modelul este rescris într-o nouă formă. În cazul nostru, ajungem t² - t - 1 ≤0. Această inegalitate trebuie rezolvată prin metoda intervalelor (aproximativ puțin mai târziu), apoi înapoi la variabila X, apoi facem același lucru cu o altă inegalitate. Răspunsurile primite vor fi soluția sistemului.

Metoda de spațiere

Aceasta este cea mai ușoară cale de a rezolva sistemele.inegalități și, în același timp, este universal și comun. Se folosește în liceu și chiar și la nivel superior. Esența lui constă în faptul că studentul caută lacune de inegalitate pe linia numărului, care este trasată într-un notebook (acesta nu este un grafic, ci doar o linie dreaptă obișnuită cu numere). În cazul în care se intersectează lacunele inegalităților, se găsește soluția sistemului. Pentru a utiliza metoda intervalului, trebuie să efectuați următorii pași:

1. Toți membrii fiecărei inegalități sunt transferați la stânga cu o schimbare a semnului la opus (zero este scris în dreapta)
2. Inegalitățile sunt scrise separat, decizia fiecăruia este determinată.
3. Există intersecții ale inegalităților pe linia numărului. Toate numerele de la aceste intersecții vor fi soluția.

Care este modul de utilizare?

Evident, cel care pare mai ușor și mai ușorconvenabil, dar există cazuri în care sarcinile necesită o anumită metodă. Cel mai adesea ei spun că este necesar să se rezolve fie cu ajutorul unui grafic, fie prin metoda intervalelor. Metoda algebrică și substituția sunt folosite extrem de rar sau deloc, deoarece sunt destul de complexe și confuze și, mai mult, sunt mai utilizate pentru a rezolva mai degrabă sisteme de ecuații decât inegalități, deci ar trebui să recurgeți la desenarea grafurilor și intervalelor. Acestea aduc vizibilitate, care nu poate decât să contribuie la implementarea eficientă și rapidă a operațiunilor matematice.

Dacă ceva nu merge

În timp ce studiază un subiect pe algebră,Firește, ar putea exista probleme cu înțelegerea ei. Și acest lucru este normal, deoarece creierul nostru este conceput astfel încât să nu poată înțelege materialul complex la un moment dat. Adesea, este necesar să citiți din nou un paragraf, să utilizați ajutorul unui profesor sau al unei practici în rezolvarea sarcinilor tipice. În cazul nostru, ei privesc, de exemplu, astfel: "Rezolvați sistemul de inegalități 3 x + 1 ≥ 0 și 2 x - 1> 3". Astfel, aspirația personală, ajutorul din afară și practică ajută la înțelegerea oricărui subiect complex.

Reshebnik?

Și un foarte bun Reshebnik, dar nupentru înșelăciune și pentru auto-ajutorare. În ele, puteți găsi un sistem de inegalități cu soluția, le uitați la ele (ca modele), încercați să înțelegeți cu exactitate modul în care autorul soluției s-a confruntat cu sarcina și apoi încercați să realizați acest lucru într-o ordine independentă.

constatări

Algebra este unul dintre cele mai dificile subiecte dinșcoala. Ei bine, ce poți să faci? Matematica a fost întotdeauna așa: este dată cuiva cu ușurință, dar pentru cineva cu dificultate. Dar, în orice caz, trebuie amintit că programul general de educație este conceput astfel încât orice student să poată face față cu acesta. În plus, trebuie să avem în vedere un număr foarte mare de asistenți. Unele dintre ele au fost menționate mai sus.