Regresia în Excel: ecuație, exemple. Regresie liniară

Analiza de regresie este o metodă statisticăUn studiu care arată dependența unui parametru de una sau mai multe variabile independente. În era de precomputer, utilizarea sa a fost destul de dificilă, mai ales atunci când era vorba de cantități mari de date. Astăzi, după ce ați învățat cum să construiți o regresie în Excel, puteți rezolva probleme statistice complexe în doar câteva minute. Mai jos sunt exemple specifice din domeniul economiei.

Tipuri de regresie

Conceptul a fost introdus în matematică de către Francis Galton în 1886. Apare regresia:

• liniar;
• parabolic;
• legea puterii;
• exponențială;
• hiperbolică;
• exponențială;
• logaritmică.

Exemplul 1

Să analizăm problema determinării dependenței numărului de membri pensionari din colectiv de salariul mediu la 6 întreprinderi industriale.

Sarcina. Șase întreprinderi au analizat salariul mediu lunar și numărul de angajați care au ieșit din proprie inițiativă. În formă tabelară avem:

	A	B	C
1	X	Numărul de resemnat	salariu
2		y	30000 de ruble
3	1	60	35.000 de ruble
4	2	35	40000 de ruble
5	3	20	45.000 de ruble
6	4	20	50.000 de ruble
7	5	15	55.000 ruble
8	6	15	60000 de ruble

Pentru problema determinării dependenței numărului de salariați care au rămas la salariul mediu la 6 întreprinderi, modelul de regresie are forma ecuației Y = a₀ + a₁x₁ + ... + a_kx_k, unde x_eu - influențarea variabilelor, a_eu - coeficienții de regresie și k - numărul de factori.

Pentru această sarcină, Y este indicatorul angajaților care au plecat, iar factorul care influențează este salariul, care este notat de X.

Utilizarea procesorului de masă Excel

Analiza regresiei în Excel trebuie precedatăaplicarea funcțiilor încorporate la datele disponibile. Cu toate acestea, pentru aceste scopuri este mai bine să folosiți pachetul de analiză foarte util. Pentru ao activa, aveți nevoie de:

• Din fila "Fișier" accesați secțiunea "Opțiuni";
• în fereastra deschisă selectați linia "Suplimente";
• Faceți clic pe butonul "Mergeți", situat în partea de jos, în partea dreaptă a liniei "Management";
• Puneți un semn de selectare lângă numele "Pachetul de analiză" și confirmați acțiunile făcând clic pe "Ok".

Dacă este făcută corect, butonul din dreapta apare în partea dreaptă a filei Date aflat deasupra foii de lucru Excel.

Regresia liniară în Excel

Acum, că avem la dispoziție toate instrumentele virtuale necesare pentru a implementa calculele econometrice, putem începe să ne rezolvăm problema. Pentru a face acest lucru:

• faceți clic pe butonul "Analiza datelor";
• în fereastra deschisă faceți clic pe butonul "Regresie";
• în fila care apare, introduceți intervalul de valori pentru Y (numărul de angajați care au plecat) și pentru X (salariul lor);
• ne confirmăm acțiunile făcând clic pe butonul "Ok".

Ca rezultat, programul va completa automatnoua analiză de regresie a datelor din procesoare de tabelă tabelară. Fiți atenți! În Excel, există posibilitatea de a stabili în mod independent locul pe care îl preferați în acest scop. De exemplu, aceasta ar putea fi aceeași foaie ca și valorile Y și X sau chiar o carte nouă proiectată special pentru a stoca astfel de date.

Analiza rezultatelor regresiei pentru R-pătrat

În Excel, datele obținute în timpul prelucrării datelor din exemplul în cauză au forma:

În primul rând, este necesar să se acorde atențievaloarea pătratului R. Este coeficientul de determinare. În acest exemplu, R-pătratul = 0.755 (75,5%), adică parametrii calculați ai modelului explică dependența dintre parametrii considerați cu 75,5%. Cu cât este mai mare valoarea coeficientului de determinare, modelul selectat este considerat mai aplicabil pentru o anumită sarcină. Se crede că descrie în mod corect situația reală cu o valoare R-pătrat peste 0,8. Dacă R-pătratul este <0,5, atunci o astfel de analiză a regresiei în Excel nu poate fi considerată rezonabilă.

Analiza coeficienților

Numărul 64.1428 arată ce va fi valoarea lui Y,dacă toate valorile xi din modelul în cauză sunt resetate. Cu alte cuvinte, se poate argumenta că valoarea parametrului analizat este influențată de alți factori care nu sunt descriși într-un anumit model.

Următorul coeficient este -0.166285, situat încelulă B18, arată efectul de ponderare al variabilei X pe Y. Aceasta înseamnă că salariul mediu lunar al angajaților din modelul în cauză afectează numărul celor care au plecat cu greutate -0,16285, adică gradul de influență este foarte mic. Semnul "-" indică faptul că coeficientul are o valoare negativă. Acest lucru este evident, deoarece toată lumea știe că cu cât este mai mare salariul la întreprindere, cu atât mai puțini oameni exprimă dorința de a rezilia contractul de muncă sau de a pleca.

Regresie multiplă

Prin acest termen se înțelege ecuația de conectare cu mai multe variabile independente ale formei:

y = f (x₁+ x₂+ ... x_m) + ε, unde y este atributul rezultat (variabila dependenta) si x₁, x₂, ... x_m - acestea sunt semne-factori (variabile independente).

Evaluarea parametrilor

Pentru regresia multiplă (MP), aceasta se realizează folosind metoda OLS (least squares). Pentru ecuațiile liniare cu forma Y = a + b₁x₁ + ... + b_mx_m+ ε construim un sistem de ecuații normale (vezi mai jos)

Pentru a înțelege principiul metodei, luați în considerare cazul cu două factori. Atunci avem o situație descrisă de formula

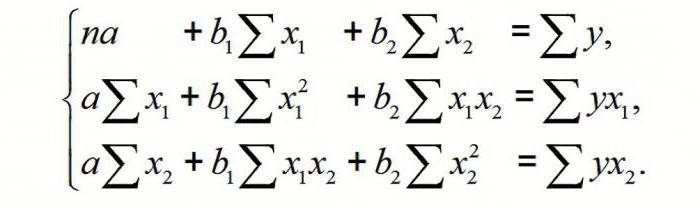
Prin urmare, obținem:

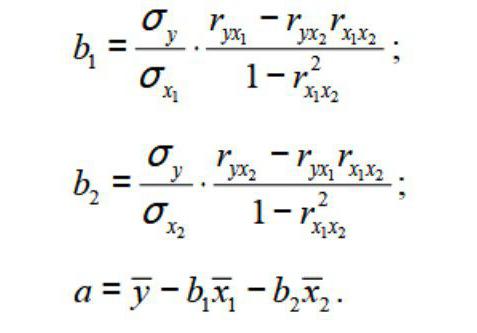
unde σ este variația caracteristicilor corespunzătoare reflectate în index.

OLS este aplicabil ecuației MP pe o scară standard. În acest caz, obținem ecuația:

în care t_y, t_{x1, ...}T_xm - variabilele standardizate pentru care mediile sunt 0; β_eu - coeficienții de regresie standardizați, iar abaterea standard este de 1.

Rețineți că toate β_eu În acest caz, acestea sunt date ca normalizate șicentralizate, astfel încât compararea lor între ele este considerată corectă și admisibilă. În plus, se obișnuiește să se creeze factori care să elimine cele care au cele mai scăzute valori ale lui βi.

Problema folosind ecuația de regresie liniară

Să presupunem că există o tabelă a dinamicii prețurilor pentru o anumită marfă N în ultimele 8 luni. Este necesar să se ia o decizie cu privire la oportunitatea achiziționării lotului său la un preț de 1850 de ruble pe tonă.

	A	B	C
1	număr de luni	numele lunii	prețul materiilor prime N
2	1	ianuarie	1750 ruble pe tonă
3	2	februarie	1755 ruble pe tonă
4	3	martie	1767 ruble pe tonă
5	4	aprilie	1760 ruble pe tonă
6	5	mai	1770 ruble pe tonă
7	6	iunie	1790 ruble pe tonă
8	7	iulie	1810 ruble pe tonă
9	8	august	1840 ruble pe tonă

Pentru a rezolva această problemă într-un procesor de masă"Excel" este necesar pentru a utiliza instrumentul deja cunoscut "Analiza datelor". Apoi selectați secțiunea "Regresie" și specificați parametrii. Trebuie amintit că în câmpul "Interval de introducere Y" trebuie introdus intervalul de valori pentru variabila dependentă (în acest caz prețurile mărfurilor în anumite luni ale anului), iar în "Interval de intrare X" - pentru numărul independent de luni. Confirmați acțiunea făcând clic pe "Ok". Pe noua foaie (dacă se specifică așa), obținem datele pentru regresie.

Construim pe ele o ecuație liniară a formei y = ax + b, undeparametrii a și b sunt coeficienții rândului cu numele numărului de luni și coeficienții și liniile "intersecția Y" din foaia cu rezultatele analizei de regresie. Astfel, ecuația de regresie liniară (VR) pentru problema 3 este scrisă ca:

Prețul mărfii N = 11,714 * numărul lunii + 1727,54.

sau în notație algebrică

y = 11,714 x + 1727,54

Analiza rezultatelor

Pentru a decide dacă ecuația rezultatăregresia liniară, coeficienții corelației multiple (KMC) și determinarea, precum și criteriul Fisher și testul Student. În tabelul Excel cu rezultate de regresie acestea apar sub numele de mai multe R, R-squared, F-statistici și t-statistici, respectiv.

KMK R face posibilă estimarea etanșeitățiiRelația probabilistică dintre variabilele independente și cele dependente. Valoarea sa ridicată indică o relație destul de puternică între variabilele "Numărul lunii" și "Prețul bunurilor N în ruble pe 1 tonă". Cu toate acestea, natura acestei relații rămâne necunoscută.

Pătratul coeficientului de determinare R²(RI) este o caracteristică numericădin distribuția totală și arată scatterul a ceea ce parte din datele experimentale, adică Valorile variabilei dependente corespund ecuației de regresie liniară. În problema examinată, această valoare este de 84,8%, adică datele statistice sunt descrise cu un grad ridicat de precizie de către SD-ul primit.

F-statistica, numită și criteriul lui Fisher, este folosită pentru a evalua semnificația dependenței liniare, respingând sau confirmând ipoteza existenței sale.

Valoarea statisticii t (Student's test) ajută la evaluarea semnificației coeficientului pentru un termen necunoscut sau liber al dependenței liniare. Dacă valoarea testului t> t_cr, atunci ipoteza nesemnificativității termenului liber al ecuației liniare este respinsă.

În problema avută în vedere pentru perioada liberăprin instrumentul de „Excel“, sa constatat că t = 169,20903, și p = 2,89E-12, t. e. au o probabilitate zero, ca credincioși va fi respins ipoteza insignifianța termenului liber. Pentru coeficientul cu t = 5.79405 necunoscut și p = 0.001158. Cu alte cuvinte, probabilitatea ca ipoteza corectă cu privire la nesemnificativitatea coeficientului pentru necunoscut să fie respinsă este de 0,12%.

Astfel, se poate argumenta că ecuația de regresie liniară rezultată este adecvată.

Problema oportunității de a cumpăra un bloc de acțiuni

Regresia multiplă în Excel se realizează utilizând același instrument "Analiza datelor". Să luăm în considerare o problemă specifică aplicată.

Compania de administrare "NNN" ar trebui să ia o deciziecu privire la oportunitatea achiziționării unei participații de 20% în MMM. Costul pachetului (SP) este de 70 de milioane de dolari SUA. Specialiștii din "NNN" au colectat date despre tranzacții similare. Sa decis să se evalueze valoarea participației la acești parametri, exprimată în milioane de dolari americani, astfel:

• conturi de plătit (VK);
• volumul cifrei de afaceri anuale (VO);
• conturi de încasat (VD);
• valoarea mijloacelor fixe (SOF).

În plus, parametrul arieratelor salariale (V3 P) este utilizat în mii de dolari SUA.

Soluție utilizând foaia de calcul Excel

Mai întâi de toate, trebuie să creați un tabel de date de intrare. Are următoarea formă:

următor:

• Apelați fereastra "Analiza datelor";
• selectați secțiunea "Regresie";
• În caseta "Interval de introducere Y" introduceți intervalul de valori al variabilelor dependente din coloana G;
• faceți clic pe pictograma cu săgeata roșie din partea dreaptă a ferestrei "Interval de introducere X" și selectați intervalul tuturor valorilor din coloanele B, C, D, F de pe foaie.

Marcați elementul "Foaie nouă de lucru" și faceți clic pe "Ok".

O analiză de regresie este obținută pentru această sarcină.

Rezultatele studiilor și concluziile

"Colectarea" din datele rotunjite prezentate mai sus pe foaia de calcul tabelar Excel, ecuația de regresie:

SP = 0,103 * SOF + 0,541 * VO - 0,031 * VK + 0,405 * VD + 0,691 * VZP - 265,844.

Într-o formă matematică mai cunoscută, ea poate fi scrisă ca:

y = 0.103 * x1 + 0.541 * x2 - 0.031 * x3 + 0.405 * x4 + 0.691 * x5 - 265.844

Datele pentru MMM sunt următoarele:

SOF, USD	VO, USD	VK, USD	VD, USD	VZP, USD	JV, USD
102,5	535,5	45,2	41,5	21,55	64,72

Înlocuindu-le în ecuația de regresie, ajungemcifra de 64,72 milioane de dolari SUA. Aceasta înseamnă că acțiunile MMM nu ar trebui să fie cumpărate, deoarece valoarea lor de 70 de milioane de dolari este destul de supraestimată.

După cum puteți vedea, utilizarea procesorului de masă Excel și a ecuației de regresie a făcut posibilă luarea unei decizii informate cu privire la fezabilitatea unei tranzacții foarte specifice.

Acum știi ce regresie este. Exemplele din Excel, discutate mai sus, vă vor ajuta în rezolvarea problemelor practice din domeniul econometriei.